The Nash equilibrium is a concept in game theory named after mathematician John Nash. It represents a stable state in a strategic interaction among multiple participants, where no individual has an incentive to change their strategy unilaterally. In other words, it is a situation where each player’s strategy is the best response to the strategies chosen by all other players.
To understand the Nash equilibrium, let’s consider a simple example: the Prisoner’s Dilemma. In this scenario, two individuals are arrested for a crime and held in separate cells. They are given the option to either cooperate with each other by remaining silent or betray each other by confessing to the crime.
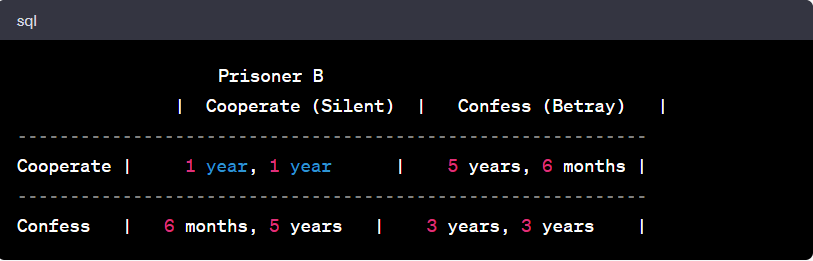
Each prisoner faces the following outcomes:
– If both prisoners remain silent (cooperate), they each receive a moderate sentence, let’s say one year in prison.
– If one prisoner remains silent while the other confesses (betrays), the prisoner who confesses will receive a reduced sentence, let’s say six months, while the one who remains silent will receive a harsh sentence, let’s say five years.
– If both prisoners confess (both betray), they will each receive a somewhat severe sentence, let’s say three years.
To analyze this situation, we can create a payoff matrix:
Each cell in the matrix represents the outcome (in terms of prison sentences) for both prisoners based on their respective choices.
To find the Nash equilibrium, we need to identify the strategies that are the best response for each player given the strategies chosen by others. In this case, we can see that if Prisoner A cooperates, Prisoner B’s best response is to confess (since they will receive a reduced sentence of six months instead of one year). Similarly, if Prisoner A confesses, Prisoner B’s best response is still to confess (since they will receive three years instead of five years).
Likewise, for Prisoner A, if Prisoner B cooperates, their best response is to confess (to receive a reduced sentence of six months instead of one year), and if Prisoner B confesses, their best response is still to confess (to receive three years instead of five years).
Therefore, in the Prisoner’s Dilemma, the Nash equilibrium is for both prisoners to confess (betray) each other. Despite the fact that both prisoners would have received lighter sentences if they had cooperated, the dominant strategy for each player is to betray the other, leading to a suboptimal outcome for both.
The Nash equilibrium concept applies not only to the Prisoner’s Dilemma but also to various other scenarios in game theory. It helps analyze strategic interactions and predict the outcomes when rational players make decisions based on their self-interest and knowledge of others’ strategies.